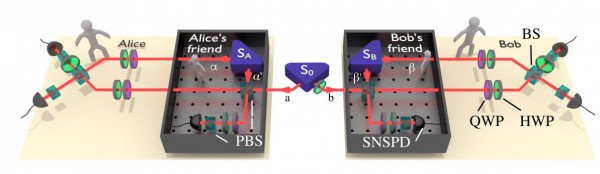
On December 3, 2018, LACMA Art + Technology Lab grant recipient Tavares Strachan launched his project ENOCH into space. Created in collaboration with LACMA, Strachan’s ENOCH is centered around the development and launch of a 3U satellite that brings to light the forgotten story of Robert Henry Lawrence Jr., the first African American astronaut selected for any national space program. In this new body of work, Strachan combines hidden histories, traditions of ancient Egypt, Shinto rituals and beliefs, and the history of exploration.
Source: ENOCH | LACMA